21 марта

Справочник 11. Математика в октавах

Автор: НИИ Центр Упреждающих Стратегий www.salvatorem.ru

11. Математика в октавах

Математические фокусы или всё ли известно о математике?

 Всем известно, каких высот достигла математика. По числу книг, статей работы по математике занимают первое место. Если в физике всё известно по структуре атома и можно смело решать любые задачи в области нанотехнологий, то в математике всё наоборот.

 Как только появился новый класс задач “Системный анализ и исследование операции”, тут же встал вопрос – как решать задачи, не используя метод перебора вариантов. В то же время созданы справочники, в том числе и справочники по решению интегралов.

 Но здесь математики не учли одну мелочь – у Вас не всегда будет под рукой необходимое вычислительное средство, которое поможет справиться со всеми необходимыми вычислениями (включая корни, логарифмы, дробные степени и прочее).

   Современная математика – это большая мусорная куча,

 при разгребании которой удаётся найти то, что надо.

 Автоматы Систем Управления Земли тоже используют математику, но там нет интегрального и дифференциального исчислений, нет рядов Тэйлора, отсутствуют функции Бесселя, Неймана и др.

 В то же время Автоматы выполняют свою работу с использованием этих наборов, но вычислительный

процесс построен по-иному.

 В качестве примера рассмотрим функцию y = 1/х. Интеграл от неё = Ln(x) + C.  Надо убрать Ln(x) и С и перевести вычисления (не только этой функции) к единой системе. Формул много, а система одна.

 Функция y = 1/x используется в пирамидах подкачки с точно дозированным значением мощности и потому вычисления должны быть простыми.

 

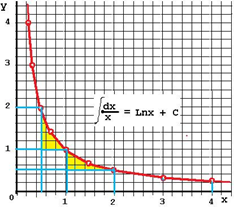
 Интеграл dx/x (границы 1 – 2) = Ln(2) = 0,69314718055994530941723212145818

 Интеграл dx/x (границы 1 – 4) = 2*Ln(2) = 1,3862943611198906188344642429164

 

 Общая формула: интеграл dx/x (нижняя граница = 1 или 20) = N*Ln(2),

 где Ln(2) – константа, точность 1280 десятичных знаков после запятой.

 

 Значение интеграла dx/x распадается на 2 части – статическую и динамическую. Используются 2 контура пирамиды.

Для N = 1 cтатическая часть = 0,5,

динамическая часть = 0,19314718055994530941723212145818.

 

 По диапазону регулирования:

 номер N

 Константа 1 = 0,69314718055994530941723212…

 Значение интеграла = константа1*N

 Статическая часть= (2N – 1)/2N или (октава-1)/октава

 Динамическая часть= значение интеграла – статическая часть.

 Константа1: точность 1280 знаков после запятой.

 Контроль: значение интеграла/константа1 = N

 

N

Октава

Значение

Статическая часть

Динамическая часть

1

2

0,6931471805599453094172321

0,5

0,1931471805599453094172321

2

4

1,3862943611198906188344642

0,75

0,6362943611198906188344642

3

8

2,0794415416798359282516963

0,865

1,2144415416798359282516963

4

16

2,7725887222397812376689284

0,9375

1,8350887222397812376689284

5

32

3,4657359027997265470861606

0,96875

2,4969859027997265470861606

6

64

4,1588830833596718565033927

0,984375

3,1745080833596718565033927

7

128

4,8520302639196171659206248

0,9921875

3,8598427639196171659206248

8

256

5,5451774444795624753378569

0,99609375

4,5490836944795624753378569

9

512

6,2383246250395077847550890

0,998046875

5,2402777500395077847550890

10

1024

6,9314718055994530941723212

0,9990234375

5,9324483680994530941723212

11

2048

7,6246189861593984035895533

0,99951171875

6,6251072674093984035895533

12

4096

8,3177661667193437130067854

0,999755859375

7,3180103073443437130067854

13

8192

9,0109133472792890224240175

0,9998779296875

8,0110354175917890224240175

14

16384

9,7040605278392343318412497

0,99993896484375

8,7041215629954843318412497

…

…

…

…

…

4096

2839,1308515735359873729827694

2838,1308515735359873729827694

 

 Для N = 4096,        статическая часть = 0.99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999 9999999999999999999999999999999999925416592687997932567090346845370661626235284653995931057284816667937216149298816950638

 2510959957219663848839674416389854658727190477469733951383517040791530851873920768121862250479592573356473705855344563493

 6085234585782739411492879968313176996777257702436300734649784662793941663483371353996387072566448153031342673500991846680

 108210421167314052581787109375

 

 Значение октавы =

134078079299425970995740249982058461274793658205923933777235614437217640300735469768018742981669034276900318581864860508

 53753882811946569946433649006084096

 

 Предел статической части = 1, значение N не превосходит 4096.

 Всё, что находится за пределами значения N = 4096, для Автоматов Комплексов является бесконечностью.

 

 Заметим, что числовые последовательности – это структуры форм устройств, используемых при проведении конкретной работы.

 

Все остальные вычисления (другие зависимости) производятся только с использованием фракталов золотого сечения, при этом октавы сохраняются.

   Следующая функция y = xx.

 Математике о ней ничего не известно, нет даже значения интеграла.

 Но эта функция – главная при построении структур клетки с использованием

 перевода в лестницу температуры. Используются фракталы золотого сечения, при этом исчезает “Arctg” и степенная зависимость.

 Математике эти способы перевода неизвестны.

 

 Пределы температурного ряда:

 Нижний предел = 12.40 (летаргический сон).

 Верхний предел для разных генотипов различен. Для генотипа 421 это значение = 66.6 (исчезновение без реинкарнации).

 

Все формулы, которые использует Система Управления Земли, разделены на 2 группы.

 Группа 1: Формулы для работы с решётками атмосферы с 12400 > h > -4400 метров.

 Группа 2: Формулы для работы с мозгом атмосферы.

 Всё остальное было сделано (и рассчитано) до установки Автоматов Управления.